Матричные операции в Excel
- © 2010 Алексей Померанцев
Содержание
- Введение
- 1. Элементарные сведения
- 1.1. Локализация
- 1.2. Книга, лист и ячейка
- 1.3. Адресация
- 1.4. Область
- 1.5. Простейшие вычисления
- 1.6. Функции
- 1.7. Некоторые важные функции
- 1.8. Ошибки в формулах
- 1.9. "Растаскивание" формул
- 1.10. Построение графиков
- 2. Матричные операции
- 2.1. Формулы массива
- 2.2. Создание и изменение формул массива
- 2.3. Простейшие операции с матрицами
- 2.4. Доступ к частям матрицы
- 2.5. Унарные операции
- 2.6. Бинарные операции
- 2.7. Регрессия
- 2.8. Критическая ошибка в Excel 2003
- 2.9. Виртуальный массив
- 3, Расширение возможностей Excel
- 3.1. Программирование. Язык VBA
- 3.2. Пример
- 3.3. Пример макроса
- 3.4. Пример пользовательской функции
- 3.5. Надстройки
- 3.6. Установка надстроек
- Заключение
Введение
В этом пособии рассказывается о программе Microsoft Excel –популярной средe для выполнения вычислений, анализа данных и построения графиков. Наша цель – познакомить читателя с базовыми возможностями, которые Excel предоставляет для обработки данных. Главное внимание уделяется работе с многомерными данными и матричным вычислениям. Отдельно рассматривается механизм надстроек (Add-in’s), расширяющих базовые возможности системы. Приведенный текст не является учебником по Excel – это всего лишь введение, краткий справочник. Более подробное изложение может быть найдено в литературе.
Сведения, приведенные в пособии, относятся к самым общим свойствам системы Excel, справедливым и для версии 2003, и для последней версии 2007. В основном, мы по-прежнему ориентируемся на пользователей старой версии 2003. Важные отличия, имеющиеся в новой версии 2007, специально оговариваются.
Изложение иллюстрируется примерами, выполненными в рабочей книге “Excel.xls ”, которая сопровождает этот документ.
Важная информация о работе с файлом Excel.xls
Ссылки на примеры помещены в текст как объекты Excel.
1. Элементарные сведения
1.1. Локализация
Программа Excel может быть использована в разных странах и на различных языках. Специфические настройки изменяют внешний вид программы, например меню, а также названия стандартных функций и способы их задания. Например, в русской версии Excel еще недавно повсеместно употреблялась запятая (,) как разделитель целой и десятичной части числа. Соответственно разделителем списков (в частности, аргументов функций) становилась точка с запятой (;). К счастью, эта практика уходит и в научных расчетах точка (.) в качестве дробного разделителя, стала общеупотребительной. – .
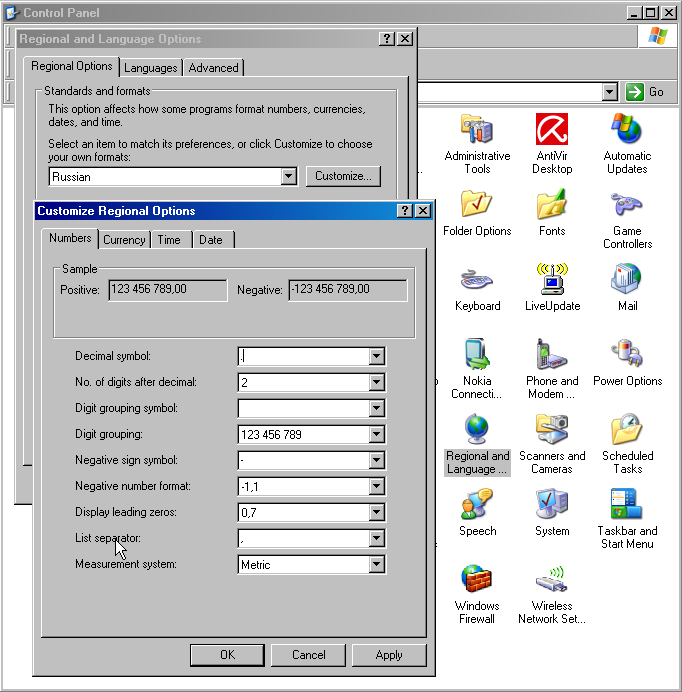
Рис. 1 Настройка региональных опций
Изменить настройки компьютера можно с помощью , через закладку с переходом на опцию Customize.
Имена встроенных в Excel функций зависят от того, какой вариант установлен – русский или английский. Например, в английской версии функция суммирования выглядит так
=SUM(A1:A9).
Эта же функция в русской версии имеет вид
=СУММ(A1:A9).
Список соответствия русско-английских имен функций приведен в файле FUNCS.XLS, который находится на вашем компьютере, обычно в директории , где – это имя версии, например Office 11. Подробнее о локализации Exсel можно прочитать здесь. В файле Excel_Functions.xls приведены имена всех функций на 16 языках.
В этом пособии мы используем английскую версию Excel 2003, в которой разделитель дробной части – точка, а разделитель списков – запятая. Русские имена функций приводятся для справки.
1.2. Книга, лист и ячейка
Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
 ,
то откроется новая пустая книга. .
,
то откроется новая пустая книга. .
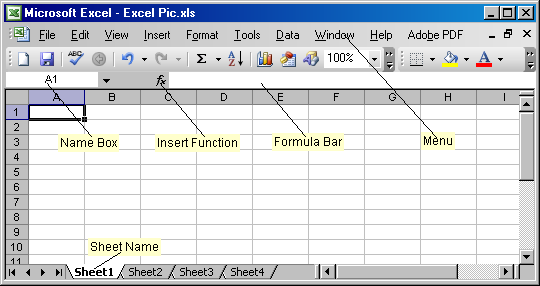
Рис. 2 Новая книга Excel
Если рабочая книга уже существует, то ее проще открыть через проводник. Для этого достаточно щелкнуть по иконке файла.
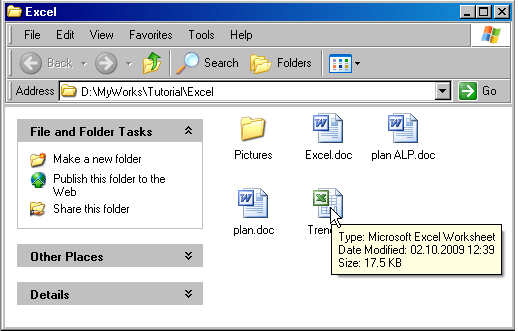
Рис. 3 Открытие книги Excel через проводник
Рабочая книга состоит из нескольких листов, имена которых показаны в нижней части окна. Листы можно удалять, добавлять, переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени листа. Появится меню, из которого можно выбрать нужную операцию.
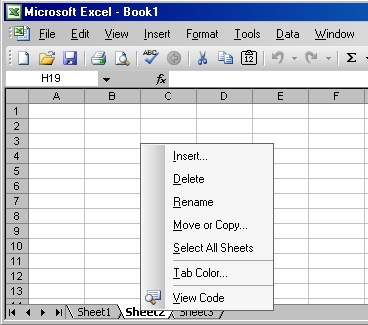
Рис. 4 Операции с листами
Стандартное имя листа – Sheet1, но ему можно дать любое имя, например Data. На лист можно вставлять рисунки, графики и другие необходимые объекты.
Каждый лист состоит из ячеек, образующих таблицу, размером 256 столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк). Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную кодировку: A, B, …,Z, AA, AB .., и т.д. до последнего столбца IV (в 2007 – до XFD). Этот стиль адресации называется A1. Реже применяется альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не будем использовать этот стиль, а прочитать об этом можно здесь
Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер: высоту или ширину.
Ячейка может иметь содержание: число, текст или формулу. Для наглядности ячейки можно форматировать: менять фонт, цвет, рамку, и т.д.
Все операции на листе выполняются с помощью меню, представленного в верхней части окна (Рис. 2). Меню в Excel 2007 существенно отличается от прежней версии. Там, вместо обычных иконок, появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому это интересно могут прочитать здесь.
1.3. Адресация
В Excel каждая ячейка имеет адрес, составленный из заголовков столбцов и строк. Например, адрес первой ячейки на листе – A1. Ячейка, находящаяся на пересечении третьего столбца и пятой строки, имеет адрес C5. Текущая ячейка выделена жирной рамкой, и ее адрес высвечивается в окне . (см. Рис. 2). Если мы хотим скопировать содержимое какой-то ячейки (например, A1) в другую клетку (например, F1), нужно во второй ячейке написать формулу =адрес, например =A1. Адресация (ссылка) может быть абсолютной, относительной и смешанной.Например, первая ячейка имеет абсолютный адрес – $A$1, относительный адрес – A1, и два смешанных адреса – $A1 и A$1. Различие в способе адресации проявляется, прежде всего, тогда, когда формула копируется и переносится в другое место. Поясним это на простом примере.



Рис. 5 Абсолютная и относительная адресация
На верхней панели Рис. 5 показан фрагмент листа с данными, выделенными желтым цветом. В зеленых областях (столбец F и строка 6) приведены различные варианты адресации одной и той же ячейки – A1 (выделена оранжевым). Тип адресации указан рядом с соответствующей ячейкой. Скопируем каждую из зеленых областей (по очереди) и вставим рядом – в соседних столбцах: G и H, и в соседних строках: 7 и 8 (средняя панель Рис. 5). Видно, что результат зависит от типа адресации. Для абсолютной адресации ссылка на первую ячейку сохранилась. Для относительной – ссылка сдвигается вправо или вниз, сохраняя относительное положение двух ячеек: той, где стоит ссылка, и той, на которую ссылаются. Для смешанной адресации результат зависит от того, куда переносится копия, и от того, какая часть адреса фиксируется значком доллара $. На правой панели показаны соответствующие формулы, получающиеся после копирования. Заметим, что ссылки на ячейки могут изменяться в зависимости от способа адресации, но при перемещении ячейки с формулой содержащиеся в формуле ссылки не изменяются.
Для адресации ячейки, которая находится на другом листе той же книги, надо указывать еще и имя листа, например: Data!B2. Восклицательный знак (!) отделяет имя листа от адреса ячейки. Если имя листа содержит пробел, тогда имя надо заключить в одинарные кавычки, например 'Raw Spectra'!C6. При адресации к другой книге, ее имя указывается впереди, в квадратных скобках, например; [Other.xls]Results!P24
Подробнее о способах адресации можно прочитать здесь.
1.4. Область
Матрица занимает на листе область. Пример показан на Рис. 6, где расположена матрица, которая имеет 9 строк (с 2 по 10) и 3 столбца (с B по D).

Рис.6 Область на листе
Для ссылки на область используется выражение, в котором адреса верхней левой и правой нижней ячеек области соединяются двоеточием. Например, B2:D10 или $B$2:$D$10.
При работе с матрицами бывает удобно присвоить ее области имя. Для этого есть два способа. Самый простой – это выделить нужную область на листе, а затем кликнуть в окно (см. Рис. 2), стереть там адрес и вписать имя – например Data (Рис. 6). Другой способ – это действовать через меню: .
Имя области может быть глобальным – доступным для любых листов книги, или локальным – определенным только для одного листа. В последнем случае, имя следует определять в форме: ListName!RangeName
Подробности смотри здесь.
1.5. Простейшие вычисления
Для проведения вычислений в Excel используются формулы. Формула начинается со знака равенства (=) и может включать в себя: ссылки, операторы, функции и константы.
Операторы позволяют проводить простейшие арифметические вычисления, примеры которых показаны на Рис. 7





Рис.7 Простейшие вычисления
1.6. Функции
Функции – это стандартные формулы, проводящие вычисления по заданным величинам, называемым аргументами. Некоторые примеры функций показаны на Рис. 8.




Рис.8 Простейшие функции
Функция состоит из имени, за которым следует круглая скобка, затем идет список аргументов, разделенных запятой и, наконец, закрывающая скобка.
Например, функция, показанная на Рис. 9 вычисляет значение кумулятивного (cumulative=TRUE), стандартного (mean=0, standard_dev =1) нормального распределения для величины, находящейся в ячейке A1 .
Рис.9 Ввод функции через Formula Bar
Задать функцию можно по-разному. Проще всего ввести ее в окно
![]() (см. Рис. 2). Только предварительно нужно открыть
это окно через меню . Такой
способ удобен, когда вы хорошо помните синтаксис функции. Формулу можно
задать быстро, т.к. аргументы вводятся простым кликаньем по ячейкам, в
которых находятся аргументы.
(см. Рис. 2). Только предварительно нужно открыть
это окно через меню . Такой
способ удобен, когда вы хорошо помните синтаксис функции. Формулу можно
задать быстро, т.к. аргументы вводятся простым кликаньем по ячейкам, в
которых находятся аргументы.
Другой способ спасает тогда, когда мы плохо помним вид
функции, которая нам нужна. Тогда удобно воспользоваться кнопкой
![]() (Рис.
2). После этого появится диалоговое окно (Рис. 10), из которого
можно выбрать нужную функцию .
(Рис.
2). После этого появится диалоговое окно (Рис. 10), из которого
можно выбрать нужную функцию .
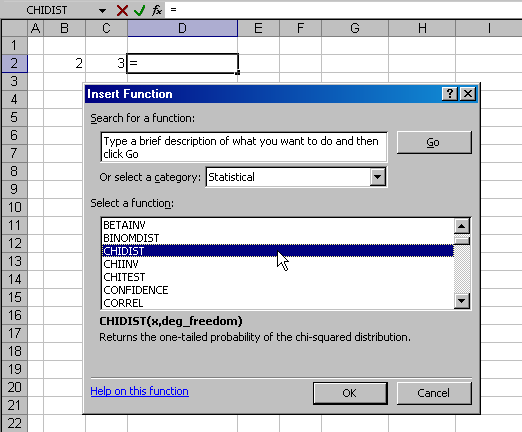
Рис.10 Ввод функции через Insert Function
Как только функция выбрана, появляется второе окно, специфическое для выбранной функции, в котором устанавливаются ссылки на аргументы функции
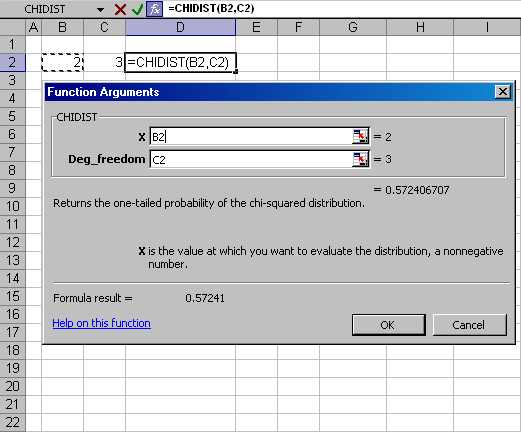
Рис.11 Задание значений аргументов
Подробнее изучить эту тему можно здесь.
1.7. Некоторые важные функции
Excel предоставляет широкий выбор стандартных (встроенных) функций. Мы не можем рассмотреть их все, поэтому остановимся только на тех, которые представляются нам самыми важными.
SUM / СУММ
Суммирует все числа в списке аргументов или в области.
Синтаксис:
SUM(number1 [,number2] [,...])
Рис.12 Функция SUM
SUMSQ / СУММКВ
Возвращает сумму квадратов аргументов.
Синтаксис:
SUMSQ(number1 [,number2] [,...])
Рис.13 Функция SUMSQ
SUMPRODUCT / СУММПРОИЗВ
Перемножает соответствующие элементы заданных массивов и возвращает сумму произведений
Синтаксис:
SUMPRODUCT (array1, array2, ...)
Рис.14 Функция SUMPRODUCT
AVERAGE / СРЗНАЧ
Возвращает среднее арифметическое своих аргументов
Синтаксис:
AVERAGE(number1 [,number2] [,...])
Рис.15 Функция AVERAGE
VAR / ДИСП
Оценивает дисперсию по выборке  .
.
Синтаксис:
VAR(number1 ,number2, ...)
Рис.16 Функция VAR
STDEV / СТАНДОТКЛОН
Оценивает стандартное отклонение по выборке
 .
.
Синтаксис:
STDEV(number1 ,number2, ...)
Рис.17 Функция STDEV
CORREL / КОРРЕЛ
Возвращает коэффициент корреляции
![]() между интервалами
ячеек array1 и array2
между интервалами
ячеек array1 и array2
Синтаксис:
CORREL(array1, array2)
Рис.17 Функция CORREL
Функции можно объединять в составные формулы, пример которой показан на Рис. 19.
Рис.19 Пример составной формулы
1.8. Ошибки в формулах
При вводе формул, а также при последующем изменении листов, возникают ошибки. При этом вместо ожидаемого результата в ячейке появляется один из символов, показанных на Рис. 20 .
Рис.20 Ошибки в формулах
Установить происхождение ошибки можно с помощью меню доступной через раздел .
Подробнее об ошибках можно прочитать здесь.
1.9. "Растаскивание" формул
При работе с данными в виде матрицы, часто возникает необходимость ввести не одну, а целую серию формул. Например, при выполнении SNV преобразования спектральных данных нужно вычислить средние значения и среднеквадратичные отклонения по каждой строке. Очень утомительно было бы повторять одну и ту же формулу многократно, меняя в ней только аргумент, даже для сильно усеченного примера, показанного на Рис. 22. А в реальных данных число строк или столбцов может доходить до десятков тысяч. К счастью это и не нужно, поскольку можно воспользоваться техникой "растаскивания" формул.
Поясним эту технику на нашем примере. Начнем с ввода формулы-образца. В этом случае – это формула, помещенная в ячейку J3 .

Рис.21 Маркер заполнения
Формулы в соседние ячейки можно вставить при помощи маркера заполнения, которым называется небольшой черный квадрат в правом нижнем углу выделенной области ячеек. При наведении мышки на этот маркер, указатель принимает вид черного креста. После этого можно перетащить ячейку, содержащую формулу, в примыкающий диапазон. Тащить можно по вертикали, как показано на Рис. 22, и по горизонтали.
Рис.22 Растаскивание серии однотипных формул
Формулы можно размножать и другим способом. Сначала копируем ячейку, содержащую формулу-образец. Потом отмечаем диапазон ячеек, в которые нужно распространить формулу, и делаем специальную вставку, выбирая опцию .
Рис.23 Копирование серии однотипных формул
Отметим, что независимо от способа, ссылки получаются правильными – на соответствующий диапазон ячеек. Это произошло потому, что в исходной формуле мы использовали относительную адресацию в аргументе: B3:I3.
Подробности можно прочитать здесь.
1.10. Построение графиков
В Excel можно строить диаграммы разных типов. Но для нас интересны только два вида: диаграмма рассеяния (scatter) и график (line). Пример диаграммы рассеяния приведен на Рис. 24 .
Рис.24 Диаграмма рассеяния
Диаграммы такого типа используются для построения графиков счетов, зависимостей "измерено-предсказано", и т.п. От линейных графиков они отличаются равноправием обеих осей. В линейных графиках ось абсцисс предназначена только для отображения категорийных переменных, т.е. величин, в которых важна не их величина, а порядок следования. Поэтому линейные графики подходят для представления зависимостей от числа главных компонент, например, для изображения того, как величины RMSEC и RMSEP меняются при усложнении модели.
Методы построения графиков в версиях 2003 и 2007 сильно отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту тему для самостоятельного изучения.
2. Матричные операции
2.1. Формулы массива
Многие операции с матрицами выполняются с помощью формул специального вида, называемыми формулами массива. От других формул они отличаются тем, что их результатом является не одна величина (число), а набор величин – массив. При вводе таких формул требуется специальное подтверждение – вместо клавиши надо нажимать комбинацию из трех клавиш .
Поясним использование формул массивов на простом примере. Предположим, что нам нужно выполнить автошкалирование (стандартизацию) данных, записанных в матрице X. Для этого сначала нужно вычислить средние значения mj и среднеквадратичные отклонения sj для каждого (j-го) столбца X, а затем вычесть из каждого столбца величину mj и поделить на величину sj
![]()
Такое преобразование можно сделать с помощью обычных формул, как это показано на Рис. 25.
Рис.25 Обычная формула
Надо только не забыть указать знак $ перед номерами строк 9 (m) и 11 (s) , чтобы зафиксировать положение соответствующих величин в строках.
Если матрица X велика, то удобнее воспользоваться формулой массива. (Рис. 26). Назовем соответствующие области на листе: X, m и s. Отметим пустую область N3:R7, размеры которой совпадают с ожидаемым результатом. После этого введем в выражение =(X-m)/s. Завершает ввод комбинация клавиш . Если все сделано правильно, то в появится формула { =(X-m)/s}, заключенная в фигурные скобки {}. Это – признак формулы массива. .
Рис.26 Формула массива
2.2. Создание и изменение формул массива
Для того чтобы правильно ввести формулу массива, нужно выделить на листе область, размеры которой совпадают с ожидаемым результатом.
Если выделить слишком большую область, то при вычислении
избыточные ячейки будут заполнены символами ошибки
#N/A. Если область вывода будет меньше, чем нужно, то часть
результатов пропадет. После выделения области, в  записывается
формула и нажимается .
записывается
формула и нажимается .
Альтернативно, сначала можно ввести формулу в одну ячейку, затем отметить область вывода, начиная с этой ячейки (право и вниз), потом перейти в и нажать .
Для того, чтобы изменить формулу массива нужно выделить область содержащую результат. Затем нужно перейти . При этом фигурные скобки вокруг формулы { } исчезнут. После этого формулу можно изменить и нажать .
Для того чтобы расширить область, которую занимает формула массива, достаточно выделить для нее новую область, перейти в и нажать . А вот для того, чтобы уменьшить эту область (например, чтобы избавиться от символов #N/A) придется потратить больше сил. Сначала нужно встать на любую ячейку области, перейти в и скопировать строку формулы. Затем нужно стереть содержимое старой области и отметить новую, меньшую область. После этого опять перейти в , вставить формулу и нажать .
Изменять отдельные ячейки в формуле массива нельзя. При попытке сделать это появляется предупреждение .

Рис.27 Предупреждение о недопустимой операции с формулой массива
2.3. Простейшие операции с матрицами
С помощью формул массива матрицы можно складывать и умножать на числа.
Рис.28 Сложение матриц и умножение на число
Для перемножения двух матриц используется функция MMULT.
2.4. Доступ к частям матрицы
Для доступа и отделения частей матрицы применяются две стандартные функции листа.
Возвращает ссылку на диапазон, отстоящий от ячейки или диапазона ячеек на заданное число строк и столбцов.
Синтаксис
OFFSET(reference, rows, cols [, height] [, width])
reference – это ссылка на область, начиная с которой вычисляется смещение;
rows – число строк, на которое надо сместиться (положительное – вниз, отрицательное вверх от начала);
cols –То же, но для столбцов (положительное – вправо, отрицательное влево от начала);
height – необязательный аргумент. Положительное число строк возвращаемой ссылки;
width – необязательный аргумент. Положительное число столбцов возвращаемой ссылки.
Примечания
-
Если аргументы height или width опущены, то предполагается, что используется такая же высота или ширина, как в аргументе reference;
-
Аргумент reference – это ссылка на область, которая должна быть реальным, а не виртуальным массивом, т.е. находиться где-то на листе.
Рис.29 Функция OFFSET
OFFSET является функцией массива и ее ввод должен завершаться нажатием комбинации .
Возвращает значения элементов в массиве, выбранных с помощью индексов строк и столбцов.
Синтаксис
INDEX (reference [, row_num] [, column_num])
reference – это массив значений (матрица);
row_num – необязательный аргумент. Номер строки, из которой берутся значения;
col_num –необязательный аргумент. Номер столбца, из которого берутся значения;
Примечания
-
Если аргумент row_num опущен, то выбирается весь столбец;
-
Если аргумент col_num опущен, то выбирается вся строка;
-
Если указаны оба необязательных аргумента, то возвращается значение, находящееся в ячейке на пересечении соответствующей строки и столбца;
-
Аргумент reference может быть ссылкой, как на область, так и на виртуальный массив.
Рис.30 Функция INDEX
INDEX является функцией массива и ее ввод должен завершаться нажатием комбинации .
2.5. Унарные операции
К матрицам можно применять следующие унарные формулы.
Возвращает обратную матрицу.
Синтаксис
MINVERSE (array)
array – это массив значений (матрица).
Примечания
-
Матрица array должна быть квадратной;
-
Если матрица вырождена, то выводится символ ошибки #VALUE!.
Рис.31 Функция MINVERSE
MINVERSE является функцией массива и ее ввод должен завершаться нажатием комбинации .
Возвращает транспонированную матрицу
Синтаксис
TRANSPOSE (array)
array– это массив значений (матрица).
Рис.32 Функция TRANSPOSE
TRANSPOSE является функцией массива и ее ввод должен завершаться нажатием комбинации .
Возвращает детерминант матрицы.
Синтаксис
MDETERM (array)
array – это массив значений (матрица).
Примечания
-
Матрица array должна быть квадратной.
MDETERM не является функцией массива и ее ввод должен завершаться нажатием одной клавиши .
2.6. Бинарные операции
К матрицам можно применять следующие бинарные операции.
Возвращает произведение двух матриц.
Синтаксис
MMULT (array1, array2)
array1, array2 – перемножаемые матрицы.
Примечания
-
Число столбцов в матрице array1 должно быть равно числу строк в матрицу array2, иначе выводится символ ошибки #VALUE!;
-
В получаемом массиве должно быть не более 5461 элементов (Excel 2003).
Рис.33 Функция MMULT
MMULT является функцией массива и ее ввод должен завершаться нажатием комбинации .
2.7. Регрессия
Для построения регрессионных зависимостей используются несколько стандартных функций листа.
Строит линейную регрессию
y=b+m1 x1+…+mJ xJ+e
Аппроксимирует известные значения вектора откликов known_y's для заданных значений матрицы предикторов known_x's и возвращает значения y, для заданного массива new_x's.
Синтаксис
TREND(known_y's [,known_x's] [,new_x's] [,const])
known_y's – вектор известных значений откликов y (калибровочный набор);
known_x's – необязательный аргумент. Матрица известных значений предикторов X (калибровочный набор);
new_x's – необязательный аргумент. Матрица новых значений предикторов Xnew (проверочный набор) для которых вычисляются и выводятся значения откликов;
const – необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы параметр b был равен нулю. Если const имеет значение TRUE или опущено, то b вычисляется обычным образом, иначе b=0.
Примечания
-
Вектор known_y's должен занимать один столбец, тогда каждый столбец матрицы массива known_x's интерпретируется как отдельная переменная;
-
Если аргумент known_x's опущен, то предполагается, что это вектор чисел {1;2;3;...} такого же размера, как и known_y's;
-
Матрица новых значений new_x's должна иметь столько же столбцов (переменных), как и матрица known_x's;
-
Если аргумент new_x's опущен, то предполагается, что он совпадает с массивом known_x's. Результат является вектором, в котором число строк равно числу строк в массиве new_x's.
Рис.34 Функция TREND
Функция TREND является функцией массива и ее ввод должен завершаться нажатием комбинации .
LINEST / ЛИНЕЙН
Дополняет функцию TREND и выводит некоторые статистические значения, связанные с регрессией
y=b+m1 x1+…+mJ xJ+e
Синтаксис
LINEST(known_y's [,known_x's] [,new_x's] [,const] [,stats])
known_y's – вектор известных значений откликов y (калибровочный набор);
known_x's – необязательный аргумент. Матрица известных значений предикторов X (калибровочный набор);
new_x's – необязательный аргумент. Матрица новых значений предикторов Xnew (проверочный набор) для которых вычисляются и выводятся значения откликов;
const – необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы параметр b был равен нулю. Если const имеет значение TRUE или опущено, то b вычисляется обычным образом, иначе b=0;
stats – необязательный аргумент. Логическое значение, которое указывает, нужно ли выводить дополнительные статистические значения. Если stats имеет значение FALSE или опущено, то выводятся только оценки коэффициентов mJ, …, m2, m1 и b . Иначе выводится целая таблица
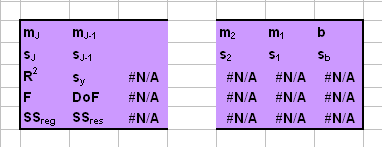
Рис. 35 Таблица вывода функция LINEST
mJ, …, m2, m1 и b – оценки регрессионных коэффициентов;
sJ, …, s2, s1 и sb – стандартные ошибки для оценок регрессионных коэффициентов;
R2 – коэффициент детерминации;
sy – стандартная ошибка оценки y;
F – F-статистика;
DoF – число степеней свободы;
SSreg – регрессионная сумма квадратов;
SSres – остаточная сумма квадратов.
Примечания
-
LINEST – это очень плохо сконструированная функция, очень неудобная в практическом применении;
-
Примечания, представленные в описании функции TREND полностью применимы к функции LINEST.
Рис.36 Функция LINEST
Функция LINEST является функцией массива и ее ввод должен завершаться нажатием комбинации .
2.8. Критическая ошибка в Excel 2003
В Excel 2003 функции TREND и LINEST при определенных условиях дают неверный результат.
Так происходит когда одновременно:
-
среднее значение по каждой переменной в матрице предикторов X равно нулю;
-
среднее значение отклика Y не равно нулю.
На Рис. 37 показан как раз такой случай: средние значения по всем столбцам матрицы Xc равны нулю, а среднее по столбцу Yc отлично от нуля..
Рис.37 Ошибка в регрессионных функциях Excel 2003
Ситуацию можно исправить, применяя функцию TREND к центрированным значениям отклика, с последующей коррекцией результата. Для этого можно использовать формулу =TREND(Yc-ym, Xc)+ym, применение которой показано на том же рисунке.
Удивительно, но эта ошибка не была замечена пользователями. Однако в новой версии 2007 она исправлена.
2.9. Виртуальный массив
При анализе данных часто возникает проблема сохранения промежуточных результатов, которые нужны не сами по себе, а только для того, чтобы вычислить по ним другие, полезные значения. Например, остатки в методе PCA часто нам не интересны, а нужны только для определения полной объясненной дисперсии, ортогональных расстояний и т.п. При этом размеры таких промежуточных массивов могут быть очень велики, да и к тому же их приходится вычислять при различных значениях числа главных компонент. Все это ведет к заполнению рабочей книги большим количеством ненужных, промежуточных результатов. Этого можно избежать, если использовать виртуальные массивы. Поясним их суть на простом примере.
Рис.38 Пример использования виртуального массива
Предположим, что задана матрица A, а нужно вычислить детерминант матрицы AtA . На Рис. 38 показаны два способа вычисления. Первый – через последовательность промежуточных массивов, отмеченных красными стрелками. Второй – с помощью одной формулы, показанной зеленой стрелкой. Оба пути ведут к одному и тому же результату, но красный путь занимает на листе много места, а зеленый последовательно использует несколько промежуточных виртуальных массивов. Все они, по сути, совпадают с реальными массивами красного пути, но на лист не выводятся.
Первый массив – это транспонированная матрица At, получаемая как результат функции TRANSPOSE(A).
Второй виртуальный массив получается тогда, когда первый виртуальный массив умножается на матрицу A с помощью функции MMULT(TRANSPOSE(A), A).
И, наконец, к этому, второму виртуальному массиву применяется функция MDETERM.
Виртуальные массивы очень полезны при вычислении всяческих вспомогательных характеристик в анализе многомерных данных: остатков, собственных значений, и т.п. Подробно об этом рассказывается в пособии Расширение возможностей Chemometrics Add-In.
3. Расширение возможностей Excel
3.1. Программирование. Язык VBA
Иногда стандартных возможностей Excel не хватает и приходится добавлять свои собственные подпрограммы. Для этой цели служит специальный язык программирования – Microsoft Visual Basic for Applications (VBA). С его помощью можно создавать макросы – наборы команд, выполняющих определенную последовательность действий, и функции – программы для специальных вычислений на листе. Макросы – это способ автоматизации стандартных процедур. Однажды создав макрос, его можно использовать для повтора рутинных действий. Обратиться к макросу можно через меню . Иногда удобно бывает приписать макрос к новой кнопке на панели инструментов или на листе.
Функции, созданные пользователем, вызываются также как и стандартные, встроенные функции – через .
Для того, чтобы макросы и пользовательские функции были доступны для применения, нужно установить соответствующий уровень безопасности через меню (Excel 2003)

Рис.39 Выбор уровня безопасности в Excel 2003
В Excel 2007 установка уровня безопасности происходит через

Рис.40 Выбор уровня безопасности в Excel 2007
Если выбран уровень (2003) или (2007), то при каждом входе в Excel система будет запрашивать разрешение на использование макросов. Мы рекомендуем установить уровни так, как показано на Рис. 39 или Рис. 40, но не пренебрегать надежным антивирусом для проверки посторонних файлов Excel.
При начальной установке Excel 2007 возможности работы с VBA сильно ограничены. Чтобы восстановить их нужно пройти по цепочке и включить опцию .
3.2. Пример
Рассмотрим вопрос о применении средств VBA на примере.
При моделировании неизотермической кинетики (ДСК, ТГА, и т.п.) необходима интегральная показательная функция (integral exponential) E1(x). По определению,

Для вычисления E1(x) можно использовать бесконечный ряд

На листе рабочей книги Excel каждый член этого ряда можно поместить в отдельную ячейку и затем просуммировать их. Этот способ показан на Рис. 41.
Рис.41 Вычисление функции E1(x) на листе
Нельзя признать такой способ вычисления удачным. Во-первых, вычисления занимают на листе много места. Но главное, не понятно, сколько членов в ряду нужно суммировать – иногда хватит и 10, а иногда и 50 будет мало.
3.3. Пример макроса
Второй способ опирается на рекуррентное соотношение, связывающее два соседних члена в ряду

Для того чтобы воспользоваться этим соотношением, надо организовать на листе рекуррентную процедуру. Например, так, как показано на Рис. 42
Рис.42 Вычисление функции E1(x) итерационным способом
Один шаг итерации – это переход от значений в области J2:J4 к значениям в области L2:L4. Для того, чтобы сделать следующую итерацию, нужно скопировать значения, получившиеся в области L2:L4 и вставить их в область J2:J4. При этом вставлять нужно только величины, без формул. Величины в области H2:H4 дают исходные значения для начала итерации .Повторяя многократно операцию , можно получить в ячейке L4 искомое значение. Однако копирование – это скучное занятие и его было бы неплохо автоматизировать. Для этого можно написать макрос.
Проще всего начать создание макроса через запись команд, выполняемых на листе. Для этого идем в раздел меню . Появляется окно (Рис. 43), в котором можно указать имя макроса и где он будет расположен.

Рис.43 Запись макро
После нажатия начинается запись всех действий, выполняемых на листе. Когда все, что нужно сохранено в макросе, запись надо остановить командой . Результат можно увидеть, зайдя в редактор Visual Basic.

Рис.44 Редактор Visual Basic
На Рис. 44 показан записанный макрос, который мы подвергли небольшому редактированию – добавили цикл для повтора операции в числе nIter раз. Величина nIter берется со страницы из ячейки J6, имеющей локальное имя n. Завершает автоматизацию кнопка , к которой привязан макрос Iteration.
Такой подход использовался нами для построения алгоритмов ITTFA и ALS в многомерном разрешении кривых.
3.4. Пример пользовательской функции
Наконец, есть еще одно, самое изящное решение проблемы с интегральной показательной функцией – написать на VBA собственную функцию листа.
Function IntExp(dX) |
Рис.45 Функция IntExp
На Рис. 45 приведен код этой функции и пример обращения к ней.
Мы не будем рассказывать о программировании на VBA, т.к. это очень большой и сложный вопрос. Самостоятельно его можно изучить по имеющимся в сети многочисленным пособиям, например, здесь.
VBA – это довольно медленный язык и он плохо подходит для больших вычислений. Например, не стоит писать на этом языке процедуру для PCA декомпозиции – на больших массивах она будет считать очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front end) для ввода и вывода данных, которые затем передаются в динамическую библиотеку (DLL), написанную на быстром языке, таком как C++ (back end). Именно эта концепция и была реализована в надстройках Fitter и Chemometrics.
Подробнее об использовании пользовательских функций для расширения возможностей надстройки Chemometrics можно прочитать здесь.
3.5. Надстройки
Написанные пользователем программы хранятся в той книге Excel, в которой они были созданы, в ее специальных разделах, называемых модулями. Для того чтобы эти макросы были доступны в других книгах, их можно туда скопировать, но можно поступить и по-другому – создать надстройку.
Надстройка – это специальный файл Excel, содержащий в себе несколько VBA модулей, связанных со всеми необходимыми библиотеками DLL. Надстройку можно подключить к системе Excel для расширения ее возможностей.
Стандартная версия Excel включает несколько надстроек, среди которых для нас примечательны две: Solver Add-In и Analysis Toolpak.
Надстройка Solver Add-In предназначена для оптимизации значения в целевой ячейке. Решение находится с помощью поиска величин в других ячейках, функционально связанных с целевой.
Надстройка Analysis Toolpak содержит набор статистических инструментов для анализа данных
В сети можно найти много надстроек для Excel, некоторые из которых распространяются свободно, другие за деньги. Вот некоторые примечательные.
J-Walk Chart Tools Add-In – бесплатная утилита для управление диаграммами: добавление подписей, ярлыков, и т.п. – все то, что отсутствует в стандартной версии.
XLStat – большой (и дорогой) пакет статистического анализа, включающий, в частности, и PLS регрессию.
Multivariate Analysis Add-in – условно бесплатный пакет для анализа многомерных данных, созданный в Бристольском университете
Fitter – надстройка для нелинейного регрессионного анализа.
Chemometrics – пакет функций листа, выполняющий анализ многомерных данных.
Подробнее о надстройках можно прочитать здесь.
3.6. Установка надстроек
Прежде чем начать использовать надстройку, нужно выполнить процедуру ее установки, которая состоит из двух частей.
В первой фазе файлы, входящие в пакет надстройки размещают на компьютере. В некоторых пакетах имеется программа Setup.exe, которая выполняет это автоматически. В других файлы нужно размещать самостоятельно. Объясним, как это нужно сделать. В состав пакета обязательно входит файл с расширением XLA и несколько вспомогательных файлов с расширениями DLL, HLP и др. Все вспомогательные файлы должны размещаться в следующих директориях: , или . Основной файл (с расширением XLA) может, в принципе, находится в любом месте, но две директории являются предпочтительными.
Microsoft рекомендует размещать файлы XLA в директории , где – это имя, под которым происходит вход в систему. Тогда этот файл можно быстро загрузить на второй фазе установки. Однако, если рабочие книги используются на нескольких компьютерах, с разными именами , то, при смене компьютера, связи с основным файлом надстройки теряются и их приходится обновлять.
Поэтому мы предлагаем поместить файл Chemometrics.xla в директорию, которая имеет одно и то же имя на разных компьютерах, например . Автоматическая установка надстройки Chemometrics Add-In описана здесь.
Вторая фаза проводится из открытой книги Excel. В версии 2003 нужно выполнить последовательность команд , а в версии 2007 последовательность: . В появившемся окне (см Рис. 45) нужно нажать и найти в компьютере нужный файл XLA.
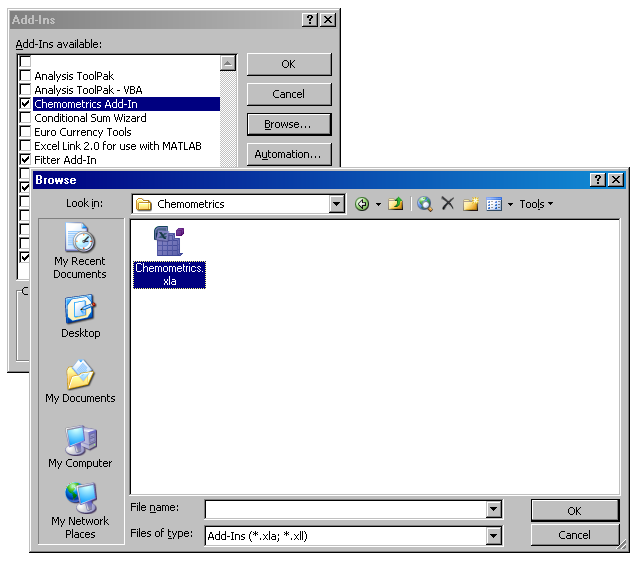
Рис.45 Установка надстройки
После того, как надстройка установлена, ее можно активировать и деактивировать устанавливая отметку напротив имени. Для удаления надстройки нужно снять галочку против ее имени в окне , закрыть Excel и удалить все ранее установленные файлы с компьютера.
Заключение
Мы рассмотрели основные приемы работы с матрицами в системе Excel. За рамками пособия осталось еще много всего важного. Частично заполнить эти пробелы поможет пособие Проекционные методы в системе Excel.



























